资金费率
资金费率热力图
多空比
大户多空比
币安/欧易/火币大户多空比
Bitfinex杠杆多空比
账号安全
资讯收藏
自选币种
密码学在加密货币中的应用
密码学是加密货币数字签名方案的基础，也是去中心化网络中双方进行安全交易验证的依据。目前，不同的加密货币采用了多种密码学方法，旨在提供高效且安全的交易模型。椭圆曲线密码学（ECC）是加密货币中最广泛使用的数字签名方案之一，而椭圆曲线数字签名算法（ECDSA）则被应用于比特币和以太坊的交易签名中。
ECC与ECDSA的背景
椭圆曲线密码学由数学家Neal Koblitz和Victor S Miller于1985年独立提出。尽管ECC是密码学领域的一项重大突破，但直到2000年代初互联网兴起时，政府和互联网服务提供商才开始将其作为一种加密方法广泛使用。
与RSA加密相比，ECC具有显著优势。ECC所需的密钥尺寸远小于RSA加密，同时仍能提供相同级别的安全性。尽管RSA加密在当今互联网中应用更为广泛，但ECC本质上是RSA的一种更高效形式，这也是其在加密货币中使用的主要原因之一。
美国国家标准与技术研究院（NIST）将ECC作为其“Suite B”推荐算法，而美国国家安全局（NSA）也正式支持使用384位密钥对绝密信息进行分类加密。例如，使用384位密钥加密机密信息时，RSA加密则需要7680位密钥。因此，ECC的效率对区块链网络非常有用，因为它可以减小交易的大小。
ECC的工作原理
椭圆曲线密码学是一种基于有限图上曲线的代数函数和结构的公钥加密方法。它利用了一种陷门函数，该函数基于从已知基点的随机椭圆曲线元素中确定离散对数的不可行性。
陷门函数在公钥密码学中被用来确保从A到B的过程是简单的，但从B到A的过程是不可行的，这是通过利用特定的数学问题实现的。例如，RSA加密基于质因数分解的概念，而ECC则依赖于点乘法的概念，其中被乘数代表私钥，并且无法从给定的起点中计算出来。
椭圆曲线由满足方程y^2 = ax^3 + b的点组成，其中(x, y)代表曲线上的一个点，a和b都是常数。理论上，可以创建无限多的曲线，但在比特币和以太坊等加密货币中，使用了一种特定的椭圆曲线，称为secp256k1。
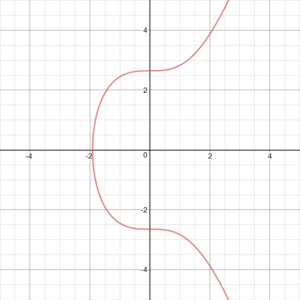
正如你所见，椭圆曲线关于x轴对称。因此，如果从曲线上的一个随机点开始画一条直线，这条直线最多会在三个点与曲线相交。你通过前两个点画一条线，并确定这条线与第三个点的交点。接下来，你将第三个点关于x轴反射（因为对称），这个点就是前两个点相加的结果。
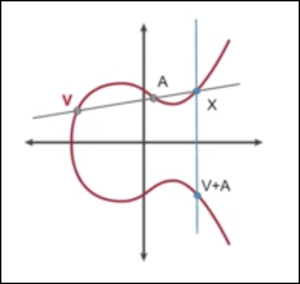
在上图中，V和A代表起点，X代表第三个点，最终点（我们称之为Z）代表V和A相加的结果。在数字签名方案中，直线的基点通常是预定义的。
为了使ECC创建陷门函数，椭圆曲线密码学使用点乘法，其中已知的基点被反复相加。在这种情况下，我们使用基点P，目标是找到2P。
在上图中，一条切线从点P穿过点R，即交点。该点的反射是2P。假设我们想继续这个过程并找到3P、4P等。接下来，我们连接P和2P，然后反射该点，并继续为4P执行此操作。
这是图的乘法属性，因为我们正在找到点是整数与点本身相乘的结果。这个结果赋予了函数其陷门，称为离散对数问题。
如果我们将变量x表示为384位整数并将其与基点P相乘，结果就是曲线上的一个点，称为Z。在加密货币中，Z是公开的，但原始变量x是秘密的（私钥）。要从Z和P中确定x，你需要确定P被加了多少次才能得到曲线上的点Z。这个问题是模算术的一种形式，在数学上是不可行的，这也是ECC如此安全的原因。
ECC在加密货币中的应用
在分析加密货币中对数字签名方案的需求时，任何给定的方案都必须满足四个主要条件，以确保其签名方案的真实性和可验证性。这些条件包括：
- 应可证明验证交易的签名者是签名者。
- 签名不应被伪造。
- 签名需要是不可否认的，即签名是最终的，不能与其他身份相关联。
- 从相应的公钥推导出私钥在计算上应该是不可行的。
椭圆曲线密码学满足了所有四个条件，并且在实现这些条件时特别有效。使用ECC时，图上点的(x, y)坐标将是你的公钥，而384位随机整数x将是你的私钥。
还可以向某人证明你知道x的值，而无需实际揭示x是什么。这一属性进一步帮助满足了在数字签名交易方案中可持续使用的必要条件。
量子计算的威胁
ECC在加密货币的数字签名方案中使用非常安全。然而，最近有人担心量子计算机的未来潜力及其强大的计算能力可能破解ECC。尽管这种可能性被认为还需要多年时间，但Shor算法理论上能够在具有足够计算能力的量子计算机上计算离散对数。
一些加密货币已经对量子计算机带来的潜在威胁采取了前瞻性的应对措施，通过实施抗量子算法作为其数字签名方案的基础。甚至NSA在2015年也宣布，由于量子计算能力的不可避免性，计划未来从ECC过渡到另一套加密算法。
结论
展望未来，加密货币的后续版本可能会逐渐过渡到更高级的加密方法来保护其交易，甚至比特币和以太坊也可能需要进行同样的过渡。
就目前而言，ECC和其他利用陷门函数的数字签名方案仍然是世界上最安全的加密方法之一，并且在未来一段时间内应继续保持这种状态。
